Atomic nuclei are charged and behave as if they were spinning on the nuclear axis, thus creating a magnetic dipole of moment µ along this axis. The angular momentum of the spinning nucleus is characterized by a spin quantum number (I). If the mass number is odd, I is ½ or an integer plus ½; otherwise, it has a value of 0 or a whole number.
Nuclei having a spin quantum number,
I 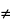
0, when placed in an external uniform static magnetic field of strength,
H0, align with respect to the field in (2
I + 1) possible orientations. Thus, for nuclei with
I = ½, which include most isotopes of analytical significance (
Table 1), there are two possible orientations, corresponding to two different energy states. A nuclear resonance is the transition between these states, by absorption or emission of the corresponding amount of energy. In a static magnetic field the nuclear magnetic axis precesses (Larmor precession) about the external field axis. The precessional angular velocity,
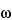 0
0, is related to the external magnetic field strength through the equation:
The energy difference between the two levels corresponds to electromagnetic radiation in the radio-frequency range. It is a function of
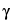
, which is a property of the nucleus, and
H0, the external field strength. As shown in
Table 1, the resonance frequency of a nucleus increases with the increase of the magnetic field strength.
NMR is a technique of high specificity but relatively low sensitivity. The basic reason for the low sensitivity is the comparatively small difference in energy between the excited and the ground states (0.02 calories at 15 to 20 kilogauss field strength), which results in a population difference between the two levels of only a few parts per million. Another important aspect of the NMR phenomenon, with negative effects on the sensitivity, is the long lifetime of most nuclei in the excited state, which affects the design of the NMR analytical test, especially in pulsed repetitive experiments. Simultaneous acquisition of the entire spectrum instead of frequency-swept spectra can give sensitivity enhancement.
Apparatus
The distinctive components of an NMR spectrometer are a magnet and a source of radio frequency. The instruments are described by the approximate resonance frequency of the analytical nucleus, e.g., 1H NMR. More recently, instruments are being referred to by their field strengths. Some spectrometers are dedicated to the analysis of one type of nucleus; others are designed to obtain spectra of different nuclei.
There are two types of commercial NMR spectrometers: the classical continuous wave (CW) instruments and the more modern pulse Fourier-transform (FT) instruments. The CW spectrometers use a technique similar to that of classical optical spectrometers: a slow scan of radio frequency (at fixed magnetic field) or of the magnetic field (at fixed radio frequency) over a domain corresponding to the resonance of the nuclei being studied. The signal generated by the absorption of energy is detected, amplified, and recorded.
Various instrument configurations are possible. The arrangement of a typical double-coil spectrometer, as one might see in the lower resolution 60-MHz and 100-MHz CW instruments, is illustrated in
Figure 1.
Fig. 1. Block diagram of a typical NMR spectrometer.
The limitations of the CW spectrometers are low sensitivity and long analysis time. In pulsed NMR spectrometers, a single pulse of radio frequency energy is used to simultaneously activate all nuclei. The excited nuclei returning to the lower energy level generate a free induction decay (FID) signal that contains in a time domain all the information obtained in a frequency domain with a CW spectrometer. The time domain and the frequency domain responses form a pair of FTs; the mathematical operation is performed by a computer after analog-to-digital conversion. After a delay allowing for relaxation of the excited nuclei, the pulse experiment (transient) may be repeated and the response coherently added in the computer memory, with random noise being averaged out. (A similar signal-to-noise increase can be obtained by combining CW spectrometers with computers that average transients.)
The block diagram of a typical high-resolution pulsed spectrometer is shown in
Figure 2.
Fig. 2. Block diagram of a typical pulsed FT-NMR spectrometer.
It is a typical configuration of the high-resolution spectrometer that uses a superconducting (cryogenic) solenoid as the source of the magnetic field. Introduction of the pulsed NMR spectrometer has made the acquisition of spectra of many nuclei, other than protons, routine. It has also allowed proton spectra to be obtained in much less time, and with smaller amounts of specimen, as compared to CW techniques.
NMR spectrometers have strict stability and homogeneity requirements. Stability is often achieved by a field-frequency locking system that “locks” the magnetic field to the resonance frequency of a reference signal. The lock signal can be homonuclear or heteronuclear. In the latter case, the reference resonance is usually a deuterium signal from a deuterated solvent. On older spectrometers, using deuterium as a locking nucleus permits noise decoupling of protons to be carried out while studying nuclei like 13C. While internal homonuclear locks are still used in CW proton spectrometers (where tetramethylsilane at about 0.5% provides a convenient lock), they are hardly ever used in pulsed FT spectrometers.
No type of magnet is capable of producing a homogeneous field over the space occupied by the specimen. Two techniques are usually employed to compensate for this lack of homogeneity: specimen spinning and the use of additional (shim) coils. Because of design, particularly probe design, the spinning in the case of the electromagnet or permanent magnet is perpendicular to the basic field. In the superconducting magnet, the axis of rotation can only be parallel to the basic magnetic field. The spin rate should be sufficient to produce averaging of the field, but not fast enough to produce an extended vortex in the specimen tube. A vortex extended near the region exposed to the radio-frequency coils decreases resolution. The shim coils are adjusted by the operator until instrumental contributions to the observed line width are minimized.
An electronic integrator is a feature of most NMR spectrometers. On a CW instrument (1H and 19F) the integrator, connected to the spectrometer output stage, determines the relative areas of the resonance peaks and presents these areas as a series of stepped horizontal lines when a sweep is made in the integration mode. On FT-NMR spectrometers, an integration algorithm is included in the spectrometer software, and the resonance peak areas may be presented graphically as stepped lines or tabulated as numeric values. The use of computer-generated tabulated/numeric integration data should not be accepted without a specific demonstration of precision and accuracy on the spectrometer in question.
The Spectrum
The signals (peaks) in an NMR spectrum are characterized by four attributes: resonance frequency, multiplicity, line width, and relative intensity. The analytical usefulness of the NMR technique resides in the fact that the same types of nuclei, when located in different molecular environments, exhibit different resonance frequencies. The reason for this difference is that the effective field experienced by a particular nucleus is a composite of the external field provided by the instrument and the field generated by the circulation of the surrounding electrons. (The latter is generally opposed to the external field and the phenomenon is called “shielding.”) In contrast with other spectroscopic methods, it is not possible to measure accurately the absolute values of transition frequencies. However, it is possible to measure accurately the difference in frequencies between two resonance signals. The position of a signal in an NMR spectrum is described by its separation from another resonance signal arbitrarily taken as standard. This separation is called chemical shift.
The chemical shift, being the difference between two resonance frequencies, is directly proportional to the magnetic field strength (or to the frequency of the oscillator). However, the ratio between the chemical shift, in frequency units, and the instrument frequency is constant. This allows definition of a dimensionless chemical shift parameter (
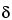
) that is independent of the instrument frequency:
in which
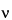 s
s is the test substance line frequency,
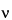 r
r is the reference line frequency,
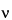 o
o is the instrument frequency, in mHz, and
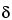 r
r is the chemical shift of the reference.
By employing the above equation, it is possible to use (with appropriate caution) the chemical shift of any known species (such as the residual 1H-containing species in deuterated solvent) as a chemical shift reference. The above equation, now in common use, is applicable to nearly all methods except in the relatively rare cases where extremely precise chemical shift values must be determined, and is readily adaptable to nuclei where non-zero reference standards are the only practical method of chemical shift determinations.
For CW instruments, tetramethylsilane (TMS) is the most widely used chemical shift reference for proton and carbon spectra. It is chemically inert, exhibits only one line, which is at a higher field than most signals, and is volatile, thus allowing for ready specimen recovery. Sodium 3-(trimethylsilyl)propionate (TSP) or sodium 2,2-dimethyl-2-silapentane-5-sulfonate (DSS) are used as NMR references for aqueous solutions. The resonance frequency of the TSP or DSS methyl groups closely approximate that of the TMS signal; however, DSS has the disadvantage of showing a number of methylene multiplets that may interfere with signals from the test substance. Where the use of an internal NMR reference material is not desirable, an external reference may be used.
Conventional NMR spectra are shown with the magnetic field strength increasing from left to right. Nuclei that resonate at high magnetic field strengths (to the right) are said to be more shielded (greater electron density) than those that resonate at lower magnetic field strengths: these are said to be de-shielded (lower electron density).
Figure 3 shows the proton NMR spectrum of 2,3-dimethyl-2-butenyl methyl ether. This compound contains protons in a methylene group (marked
d in the graphic formula) and in four methyl groups (
a,
a,
b, and
c). Methyl groups
b and
c are situated in distinctly different molecular environments than the two
a methyl groups. Three different methyl proton resonances are observed as spectral peaks in addition to the peak corresponding to methylene proton resonance. The two
a methyl groups, being in very similar environments, have the same chemical shift. Interaction between magnetically active nuclei situated within a few bond lengths of each other leads to coupling, which results in a mutual splitting of the respective signals into sets of peaks or multiplets.
Fig. 3. NMR spectrum of 2,3-dimethyl-2-butenyl methyl ether (15% in CCl
4) showing four nonequivalent, apparently uncoupled protons with a normal integral trace (peak area ratio from low
H0 to high
H0 of 2:3:3:6). (Tetramethylsilane, the NMR Reference, appears at 0 ppm.) The system of units represented by
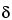
is defined under
The Spectrum, in this chapter.
The coupling between two nuclei may be described in terms of the spin-spin coupling constant, J, which is the separation (in hertz) between the individual peaks of the multiplet. Where two nuclei interact and cause reciprocal splitting, the measured coupling constants in the two resulting mutiplets are equal. Furthermore, J is independent of magnetic field strength.
In a first-order, comparatively noncomplex spin system, the number of individual peaks that are expected to be present in a multiplet and the relative peak intensities are predictable. The number of peaks is determined by 2
nI + 1, where
n is the number of nuclei on adjacent groups that are active in splitting. For protons this becomes (
n + 1) peaks. In general, the relative intensity of each peak in the multiplet follows the coefficient of the binomial expansion (
a +
b)
n. These coefficients may conveniently be found by use of Pascal's triangle, which produces the following relative areas for the specified multiplets: doublet, 1:1; triplet, 1:2:1; quartet, 1:3:3:1; quintet, 1:4:6:4:1; sextet, 1:5:10:10:5:1; and septet, 1:6:15:20:15:6:1. This orderly arrangement, generally referred to as first-order behavior, may be expected when the ratio of D
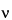
to
J is greater than about 10; D
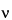
is the chemical shift difference between two nuclei or two groups of equivalent nuclei. Two examples of idealized spectra arising from first-order coupling are shown in
Figure 4.
Fig. 4. Diagrammatic representation of simple first-order coupling of adjacent protons.
Figure 5 shows a spectrum displaying triplet signals resulting from the mutual splitting of two adjacent methylene groups.
Fig. 5. NMR spectrum of 3-keto-tetrahydrofuran (10% in CCl4) showing three nonequivalent protons, with a normal integral trace (peak area ratio from low H0 to high H0 of 1:1:1). Note two sets of methylene groups coupled to each other at 4.2 and 2.4 ppm. (Tetramethylsilane, the NMR Reference, appears at 0 ppm.)
Coupling may occur between 1H and other nuclei, such as 19F, 13C, and 31P. In some cases, e.g., in the CW mode, the coupling constants may be large enough so that part of the multiplet is off scale at either the upfield or downfield end. This type of coupling may occur over the normal “three-bond distance,” as for 1H-1H coupling.
Magnetically active nuclei with
I 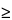
1, such as
14N, possess an electrical quadrupole moment, which produces line-broadening of the signal due to neighboring nuclei.
Another characteristic of the signal, its relative intensity, has wide analytical applications. In carefully designed experiments (see the section General Method), the area or intensity of a signal is directly proportional to the number of protons giving rise to the signal. As a result, it is possible to determine the relative ratio of the different kinds of protons or other nuclei in a specimen or to perform NMR assays with the aid of an internal standard.
The NMR spectra may contain extraneous signals due to the inhomogeneity of the magnetic field throughout the specimen. These artifacts, called spinning side bands, appear as minor lines symmetrically located around each signal. The presence of large spinning side bands indicates that the non-spinning shims require adjustment. The separation is equal to the frequency of the specimen tube spin rate or some integral multiple of that frequency. Thus, spinning side bands are readily identifiable.
General Method
Inadequate specimen preparation or incorrect instrumental adjustments and parameters may lead to poor resolution, decreased sensitivity, spectral artifacts, and erroneous data. It is preferable that the operator be familiar with the basic theory of NMR, the properties of the specimen, and the operating principles of the instruments. Strict adherence to the instruction manuals provided by the manufacturer and frequent checks of the performance of the instrument are essential.
The method and procedures discussed here refer specifically to 1H (proton) and 19F NMR. They are applicable, with modification, to other nuclei. The discussion presumes that the NMR spectra are obtained from liquid test substances or solutions in suitable solvents.
Selection of Solvent—
In addition to having good solubility properties, suitable solvents do not exhibit resonance peaks that obscure resonance peaks of the specimen being analyzed. The most commonly used solvents for proton and carbon NMR are listed in
Table 2. Deuterated solvents also provide the signal for the heteronuclear system lock. If solvent peaks might interfere with any signals from the specimen, then the isotopic purity of the solvent should be as high as possible. Deuterium (
I = 1) does not exhibit resonance under
1H conditions but may cause
J-coupling to be observed. The residual protons generate solvent peaks whose chemical shifts are shown in
Table 2.
Table 2. Solvents Commonly Used for Proton NMR
| Solvent |
Residual Proton Signal, 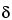 a a |
| CCl4b |
— |
| CS2b |
— |
| SO2 (liquid) |
— |
| (CF3)2CO |
— |
| CDCl3 |
7.27 |
| CD3OD |
3.35, 4.8 c |
| (CD3)2CO |
2.05 |
| D2O |
4.7 c |
| DMSO-d6 d |
2.50 |
| C6D6 |
7.20 |
| p-Dioxane-d8 |
3.55 |
| CD3CO2D |
2.05, 8.5 c |
| DMF-d7e |
2.77, 2.93, 8.05 |
a
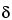 in ppm relative to tetramethylsilane arbitrarily taken as 0 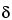 or 0 ppm.
b
Spectrophotometric grade.
c
Highly variable; depends on solute and temperature.
d
Dimethyl sulfoxide-d6.
e
N,N-Dimethylformamide-d7 per Aldrich, Alfa, Fluka, and Sigma catalogs.
|
Some solvents (e.g., D2O or CD3OD) enter into fast exchange reactions with protons and may eliminate resonance signals from –COOH, –OH, and –NH2 structural groups. The protons in alcohols and amines do not take part in rapid exchange unless catalyzed by small concentrations of acid or base, except in the presence of D2O and some other solvents (e.g., CD3OD).
For 19F NMR, most solvents used in proton NMR may be employed, the most common ones being CHCl3, CCl4, H2O, CS2, aqueous acids and bases, and dimethylacetamide. In general, any nonfluorinated solvent may be used, provided that it is of spectral quality. Obviously, there is no interference from the protonated functional groups of the solvent. However, unless they are decoupled, protonated functional groups on the 19F-containing specimen will provide J-coupling.
Specimen Preparation—
Directions are usually given in individual monographs. The solute concentration depends on the objective of the experiment and on the type of instrument. Detection of minor contaminants may require higher concentrations. The solutions are prepared in separate vials and transferred to the NMR specimen tube. The volume required depends on the size of the specimen tube and on the geometry of the instrument. The level of the solution in the tube must be high enough to extend beyond the coils when the tube is inserted in the instrument probe and spun.
The NMR specimen tubes must meet narrow tolerance specifications in diameter, wall thickness, concentricity, and camber. The most widely used tubes have a 5- or 10-mm outside diameter and a length of between 15 and 20 cm. Microtubes are available for the analysis of small amounts of specimen.
Procedure—
The specimen tube is placed in a probe located in the magnetic field. The probe contains electronic circuitry including the radio-frequency coil(s), and is provided with attachments for the air supply that spins the specimen tubes.
Instrument adjustments are made before each experiment. The spinning rate of the specimen tube is adjusted so that spinning side bands do not interfere with the peaks of interest and the vortex does not extend beyond the coils in the probe. To optimize the instrument performance, the magnetic shim gradients on FT-NMR spectrometers are adjusted. In adjusting resolution on CW spectrometers, a good indicator is the definite “ringing” of the TMS peak. The phenomenon of ringing is the oscillation of the recorder trace after the magnetic field has passed through a resonance frequency. Ringing, evident on a number of the peaks in Figures 5 and 6, arises during rapid scans and decays exponentially to the baseline value.
Fig. 6. Continuous wave proton spectrum of ethyl ether.
Figure 7 clearly indicates the absence, in an FT experiment, of the ringing phenomenon. Ringing will not appear because the spectrum obtained is the result of analysis of the FID by Fourier transformation and not a magnetic field or frequency sweep through the individual resonance positions.
Fig. 7. Proton NMR spectrum of ethyl ether in deuterated chloroform.
With proton CW instruments the spectrum is scanned from 0 ppm to about 10 ppm with a scan time of about 1 to 5 minutes. The amplification is adjusted so that all peaks remain on scale. If the response is low at reasonable amplitude, the radio-frequency power is increased to obtain the highest possible peak response without peak broadening. After the initial scan, the presence of peaks downfield of 10 ppm is quickly checked by off-setting the instrument response by about 5 ppm. With CW instrumentation, it is common for the TMS peak to shift slightly during an extended scan. The extent of the shift is usually obtained by comparing the relative positions of another peak in the initial scan with the same peak in the offset scan.
The operation of an FT-NMR spectrometer is a much more elaborate experiment. The computer serves to control the spectrometer, to program the experiment, and to store and process the data. Programming the experiment involves setting values for a large number of variables including the spectral width to be examined, the duration (“width”) of the excitation pulse, the time interval over which data will be acquired, the number of transients to be accumulated, and the delay between one acquisition and the next. The analysis time for one transient is in the order of seconds. The number of transients is a function of the specimen concentration, the type of nucleus, and the objective of the experiment. At the end of the experiment, the FID signal is stored in digitized form in the computer memory and is displayed on the video screen. The signal can be processed mathematically to enhance either the resolution or the sensitivity, and it can be Fourier-transformed into a frequency-domain spectrum. The instrument provides a plot of the spectrum. The integration routine, accessed through keyboard commands, results in a stepped-line plot. Considerably more accurate integrals are obtained if the signals or regions of interest are separately integrated.
FT-NMR spectrometers may yield qualitative and quantitative data from the same experiment, but this is seldom done in practice. In quantitative FT experiments, special precautions must be taken for the signal areas to be proportional to the number of protons. The delays between pulses must be long enough to allow complete relaxation of all excited nuclei. This results in a considerable increase in analysis time and in some loss of resolution. Qualitative analysis is usually performed in nonquantitative conditions, with the design of the experiment directed to fast analysis with maximum resolution or sensitivity.
Qualitative and Quantitative Analysis
NMR spectroscopy has been used for a wide range of applications such as structure elucidation; thermodynamic, kinetic, and mechanistic studies; and quantitative analysis. Some of these applications are beyond the scope of compendial methods.
All five characteristics of the signal—chemical shift, multiplicity, line width, coupling constants, and relative intensity—contribute analytical information.
Qualitative Applications—
Comparison of a spectrum from the literature or from an authentic specimen with that of a test specimen may be used to confirm the identity of a compound and to detect the presence of impurities that generate extraneous signals. The NMR spectra of simple structures can be adequately described by the numeric value of the chemical shifts and coupling constants, and by the number of protons under each signal. (The software of modern instruments includes programs that generate simulated spectra using these data.) Experimental details, such as the solvent used, the specimen concentration, and the chemical shift reference, must also be provided.
For unknown specimens, NMR analysis, usually coupled with other analytical techniques, is a powerful tool for structure elucidation. Chemical shifts provide information on the chemical environment of the nuclei. Extensive literature is available with correlation charts and rules for predicting chemical shifts. The multiplicity of the signals provides important stereochemical information. Mutual signal splitting of functional groups indicates close proximity. The magnitude of the coupling constant, J, between residual protons on substituted aromatic, olefinic, or cycloalkyl structures is used to identify the relative position of the substituents.
Several special techniques (double resonance, chemical exchange, use of shift reagents, two-dimensional analysis, etc.) are available to simplify some of the more complex spectra, to identify certain functional groups, and to determine coupling correlations.
Double resonance, or spin decoupling, is a technique that removes the coupling between nuclei and thus simplifies the spectrum and identifies the components in a coupling relationship. For example, in a simple two-proton system, generally designated an AX system (see
Figure 4), each proton appears as a doublet. If a strong radio-frequency field is introduced at the frequency of X, while the normal radio-frequency field is maintained at the frequency that causes A to resonate, the coupling between A and X is removed (homonuclear decoupling). A is no longer split, but instead appears as a singlet. Routine
13C spectra are obtained under proton decoupling conditions that remove all heteronuclear
13C-
1H couplings. As a result of this decoupling, the carbon signals appear as singlets, unless other nuclei that are not decoupled are present (e.g.,
19F,
31P).
Functional groups containing exchangeable protons bound to hetero-atoms such as –OH, –NH2, or –COOH groups may be identified by taking advantage of the rapid exchange of these protons with D2O. To determine the presence and position of these groups, scan the test substance in CDCl3 or DMSO-d6, then add a few drops of D2O to the specimen tube, shake, and scan again. The resonance peaks from these groups collapse in the second scan and are replaced by the HDO singlet between 4.7 and 5.0 ppm.
This chemical exchange is an example of the effect of intermolecular and intramolecular rate processes on NMR spectra. If a proton can experience different environments by virtue of such a process (tautomerism, rotation about a bond, exchange equilibria, ring inversion, etc.), the appearance of the spectrum will be a function of the rate of the process. Slow processes (on an NMR time scale) result in more than one signal, fast processes average these signals to one line, and intermediate processes produce broad signals.
The software of modern FT-NMR spectrometers allows for sequences of pulses much more complex than the repetitive accumulation of transients described above. Such experiments include homonuclear or heteronuclear two-dimensional analysis, which determines the correlation of couplings and may simplify the interpretation of otherwise complex spectra.
Quantitative Applications—
If appropriate instrument settings for quantitative analysis have been made, the areas (or intensities) of two signals are proportional to the total number of protons generating the signals.
If the two signals originate from two functional groups of the same molecule, the equation can be simplified to
in which n1 and n2 are the number of protons in the respective functional groups.
If the two signals originate from different molecular species,
where m1 and m2 are the numbers of moles; W1 and W2 are the masses; and M1 and M2 are the molecular weights of compounds 1 and 2, respectively.
Examination of Equations 2 and 3 shows that NMR quantitative analysis can be performed in an absolute or relative manner. In the absolute method, an internal standard is added to the specimen and a resonance peak area arising from the test substance is compared with a resonance peak area from the internal standard. If both test substance and internal standard are accurately weighed, the absolute purity of the substance may be calculated. A good internal standard has the following properties: it presents a reference resonance peak, preferably a singlet, at a field position removed from all specimen peaks; it is soluble in the analytical solvent; its proton equivalent weight, i.e., the molecular weight divided by the number of protons giving rise to the reference peak, is low; and it does not interact with the compound being tested. Typical examples of useful standards are 1,2,4,5-tetrachlorobenzene, 1,4-dinitrobenzene, benzyl benzoate, and maleic acid. The choice of a standard will be dictated by the spectrum of the specimen.
The relative method may be used to determine the molar fraction of an impurity in a test substance (or of the components in a mixture) as calculated by Equation 3.
Quantitative analysis, as well as detection of trace impurities, is markedly improved with modern instrumentation. Stronger magnetic fields and the ability to accumulate and/or average signals over long periods of time greatly enhance the sensitivity of the method.
Absolute Method of Quantitation—
Where the individual monograph directs that the
Absolute Method of Quantitation be employed, proceed as follows.
Solvent, Internal Standard, and NMR Reference—
Use as directed in the individual monograph.
Test Preparation—
Transfer an accurately weighed quantity of the test substance, containing about 4.5 proton mEq, to a glass-stoppered, graduated centrifuge tube. Add about 4.5 proton mEq of Internal Standard, accurately weighed, and 3.0 mL of Solvent, insert the stopper, and shake. When dissolution is complete, add about 30 µL (30 mg if a solid) of NMR Reference, provided that it does not interfere with subsequent measurements, and shake.
Procedure—
Transfer an appropriate amount (0.4 to 0.8 mL) of
Test Preparation to a standard 5-mm NMR spinning tube, and record the spectrum, adjusting the spin rate so that no spinning side bands interfere with the peaks of interest. Measure the area under each of the peaks specified in the individual monograph by integrating not fewer than five times. Record the average area of the
Internal Standard peak as
AS and that of the
Test Preparation peak as
AU.
Calculate the quantity, in mg, of the analyte in the Test Preparation by the formula:
in which WS is the weight, in mg, of Internal Standard taken; and EU and ES are the proton equivalent weights (i.e., the molecular weights divided by the number of protons giving rise to the reference peak) of the analyte and the Internal Standard, respectively.
Relative Method of Quantitation—
Where the individual monograph directs that the
Relative Method of Quantitation be employed, proceed as follows.
Solvent, NMR Reference, and Test Preparation—
Use as directed under Absolute Method of Quantitation.
Procedure—
Transfer an appropriate amount (0.4 to 0.8 mL) of
Test Preparation to a standard 5-mm NMR spinning tube, and record the spectrum, adjusting the spin rate so that no spinning side bands interfere with the peaks of interest. Measure the area or intensity under each of the peaks specified in the individual monograph by integrating not fewer than five times. Record the average area or intensity resulting from the resonances of the groups designated in the individual monograph as
A1 and
A2.
Calculate the quantity, in mole percent, of the analyte in the Test Preparation by the formula:
in which n1 and n2 are, respectively, the numbers of protons in the designated groups.