Designs for Minimizing the Error Variance—
Variation in response is reduced as much as is practicable by the limitations imposed on body weight, age, previous handling, environment, and similar factors. In a number of assays, the test animals or their equivalent are then assigned at random but in equal numbers to the different doses of the Standard and Unknown. This implies an objective random process, such as throwing dice, shuffling cards, or using a table of random numbers. Assigning the same number of individuals to each treatment simplifies the subsequent calculations materially, and usually leads to the shortest confidence interval for a given number of observations.
In some assays, the potential responses can be assembled into homogeneous sets in advance of treatment. The differences between sets are later segregated, so that they do not affect adversely either the computed potency or its confidence interval. One unit within each set, picked at random, receives each treatment. Examples of randomized sets are the cleared areas on a single plate in the plate assay of an antibiotic, and four successive paired readings in the same rat in the Vasopressin Injection assay. Sets of two occur where each test animal is used twice, as in the assays of Tubocurarine Chloride Injection and Insulin Injection. In these cases, neither the average differences between individuals nor the order of treatment can bias the potency or precision. In the microbial assays for vitamin B12 activity and for calcium pantothenate, replicate tubes are assigned to two or more separate, complete sets, preferably with the tubes arranged at random within each set. This restricts the variation due to position or order within a set to the differences within each complete replicate.
Rejection of Outlying or Aberrant Observations—
A response that is questionable because of failure to comply with the procedure during the course of an assay is rejected. Other aberrant values may be discovered only after the responses have been tabulated, but can then be traced to assay irregularities, which justify their omission. The arbitrary rejection
or retention of an apparently aberrant response can be a serious source of bias. In general, the rejection of observations solely on the basis of their relative magnitudes is a procedure to be used sparingly. When this is unavoidable, each suspected aberrant response or outlier may be tested against one of two criteria:
1. The first criterion is based upon the variation within a single group of supposedly equivalent responses. On the average, it will reject a valid observation once in 25 or once in 50 trials, provided that relatively few, if any, responses within the group are identical. Beginning with the supposedly erratic value or outlier, designate the responses in order of magnitude from
y1 to
yN, where
N is the number of observations in the group. Compute the relative gap
G1 = (
y2 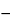 y1
y1)/(
yN 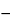 y1
y1) when
N = 3 to 7,
G2 = (
y3 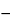 y1
y1)/(
yN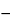 1
1 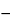 y1
y1) when
N = 8 to 13, or
G3 = (
y3 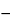 y1
y1)/(
yN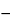 2
2 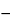 y1
y1) when
N = 14 to 24. If
G1,
G2, or
G3 exceeds the critical value in
Table 1 for the observed
N, there is a statistical basis for omitting the outlier.
Table 1
| Test for outliers. In samples from a normal population, gaps equal to or larger than the following values of G1, G2, and G3 occur with a probability P = 0.02 where outliers can occur only at one end, or with P = 0.04 where they may occur at either end. |
|
|
|
|
|
|
|
|
|
|
|
|
| N |
3 |
4 |
5 |
6 |
7 |
|
|
|
|
|
|
| G1 |
.976 |
.846 |
.729 |
.644 |
.586 |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| N |
8 |
9 |
10 |
11 |
12 |
13 |
|
|
|
|
|
| G2 |
.780 |
.725 |
.678 |
.638 |
.605 |
.578 |
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| N |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
| G3 |
.602 |
.579 |
.559 |
.542 |
.527 |
.514 |
.502 |
.491 |
.481 |
.472 |
.464 |
This criterion is applicable also in a microbial assay where each treatment is represented by a transmittance in each of two separate complete sets. Subtract each transmittance in the first set from its paired value in the second set, and record each difference with its sign, either plus or minus. Beginning with the most divergent difference, designate the
N differences in order of magnitude from
y1 to
yN and compute the relative gap
G1,
G2, or
G3. If this exceeds its critical value in
Table 1, one of the two transmittances giving the aberrant difference is suspect and may be identified on inspection or by comparison with its expectation (see next column). Repeat the process with the remaining differences if an outlier is suspected in a second pair.
2. The second criterion compares the ranges from a series of
k = 2 or more groups. Different groups may receive different treatments, but all
f responses within each group represent the same treatment. Compute the range from each group by subtracting the smallest response from the largest within each of the
k groups. Divide the largest of the
k ranges by the sum of all the ranges in the series. Refer this ratio
R* to
Table 2. If
k is not larger than 10, use the tabular values in the upper part of
Table 2; if
k is larger than 10, multiply
R* by (
k + 2) and interpolate, if necessary, between the tabular values in the lower part of
Table 2. If
R* exceeds the tabular or interpolated value, the group with the largest range is suspect and inspection of its components will usually identify the observation, which is then assumed to be aberrant or an outlier. The process may be repeated with the remaining ranges if an outlier is suspected in a second group.
Table 2
Test for groups containing outliers. Compute the range from the f observations in each of k groups, where all groups in the series are equal in size. The observed ratio R* of the largest range to the sum of the k ranges will equal or exceed the following critical values at a probability of
P = 0.05. |
| No. of Ranges k |
Critical R* for Ranges Each from f Observations |
| 2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| |
|
|
|
|
|
|
|
|
|
| 2 |
0.962 |
0.862 |
0.803 |
0.764 |
0.736 |
0.717 |
0.702 |
0.691 |
0.682 |
| 3 |
.813 |
.667 |
.601 |
.563 |
.539 |
.521 |
.507 |
.498 |
.489 |
| 4 |
.681 |
.538 |
.479 |
.446 |
.425 |
.410 |
.398 |
.389 |
.382 |
| 5 |
.581 |
.451 |
.398 |
.369 |
.351 |
.338 |
.328 |
.320 |
.314 |
| |
|
|
|
|
|
|
|
|
|
| 6 |
0.508 |
0.389 |
0.342 |
0.316 |
0.300 |
0.288 |
0.280 |
0.273 |
0.267 |
| 7 |
.451 |
.342 |
.300 |
.278 |
.263 |
.253 |
.245 |
.239 |
.234 |
| 8 |
.407 |
.305 |
.267 |
.248 |
.234 |
.225 |
.218 |
.213 |
.208 |
| 9 |
.369 |
.276 |
.241 |
.224 |
.211 |
.203 |
.197 |
.192 |
.188 |
| 10 |
.339 |
.253 |
.220 |
.204 |
.193 |
.185 |
.179 |
.174 |
.172 |
| No. of Ranges k |
Critical (k + 2)R* for Ranges Each from f Observations |
| 2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| |
|
|
|
|
|
|
|
|
|
| 10 |
4.06 |
3.04 |
2.65 |
2.44 |
2.30 |
2.21 |
2.14 |
2.09 |
2.05 |
| 12 |
4.06 |
3.03 |
2.63 |
2.42 |
2.29 |
2.20 |
2.13 |
2.07 |
2.04 |
| 15 |
4.06 |
3.02 |
2.62 |
2.41 |
2.28 |
2.18 |
2.12 |
2.06 |
2.02 |
| 20 |
4.13 |
3.03 |
2.62 |
2.41 |
2.28 |
2.18 |
2.11 |
2.05 |
2.01 |
| 50 |
4.26 |
3.11 |
2.67 |
2.44 |
2.29 |
2.19 |
2.11 |
2.06 |
2.01 |
Replacement of Missing Values—
As directed in the monographs and in this section, the calculation of potency and its confidence interval from the total response for each dose of each preparation requires the same number of observations in each total. When observations are lost or additional responses have been obtained with the Standard, the balance may be restored by one of the following procedures, so that the usual equations apply.
1. Reduce the number of observations in the larger groups until the number of responses is the same for each treatment. If animals have been assigned at random to each treatment group, either omit one or more responses, selected at random, from each larger group, or subtract the mean of each larger group from its initial total as often as may be necessary. The latter technique is preferred when extra animals have been assigned deliberately to the Standard. When the assay consists of randomized sets, retain only the complete sets.
2. Alternatively, an occasional smaller group may be brought up to size when the number of missing responses is not more than one in any one treatment or 10% in the entire assay. Estimate a replacement for each missing value by either method a or method b. One degree of freedom (n) is lost from the error variance s2 for each replacement by either method, except in a microbial assay where each response is based on the sum of two or more transmittances and only one transmittance is replaced.
(a) If animals have been assigned to treatments at random, add the mean of the remaining responses in the incomplete group to their total. In a microbial assay, when one of two transmittances is missing for a given treatment, add the mean difference between sets, computed from all complete pairs, to the remaining transmittance to obtain the replacement.
(b) If the assay consists of randomized sets, replace the missing value by
where f is the number of sets, k is the number of treatments or doses, and Tr¢, Tt¢, and T ¢ are the incomplete totals for the randomized set, treatment, and assay from which an observation is missing.
If the assay consists of n¢ Latin squares with k rows in common, replace a missing value by
where n¢ is the number of Latin squares with k rows in common, k is the number of treatments or doses, and Tc¢, Tr¢, Tt¢, and T ¢ are respectively the incomplete totals for the column, row, treatment, and assay from which an observation is missing.
If more than one value is missing, substitute the treatment mean temporarily in all but one of the empty places, and compute y¢ for the other by Equation 1. Replace each of the initial substitutions in turn by Equation 1, and repeat the process in successive approximations until a stable y¢ is obtained for each missing observation.