| A |
absorbance for computing % reduction in bacte-
 rial growth from turbidimetric readings. rial growth from turbidimetric readings. |
| b |
slope of the straight line relating response (y) to
 log-dose (x) [Equations 2b, 4, 5, 6]. log-dose (x) [Equations 2b, 4, 5, 6]. |
| c |
constant for computing M¢ with Equations 8
 and 10. and 10. |
| c¢ |
constant for computing L with Equations 26
 and 29. and 29. |
| ci |
constant for computing M¢ when doses are spaced
 as in Table 8. as in Table 8. |
| c¢i2 |
constant for computing L when doses are spaced
 as in Table 8. as in Table 8. |
| C |
term measuring precision of the slope in a
 confidence interval [Equations 27, 28, 35, 36]. confidence interval [Equations 27, 28, 35, 36]. |
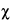 2 2 |
statistical constant for testing significance of a
 discrepancy [Table 9]. discrepancy [Table 9]. |
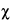 M2 M2 |
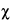 2 testing the disagreement between different 2 testing the disagreement between different
 estimates of log-potency [Equations 39, 40]. estimates of log-potency [Equations 39, 40]. |
| eb |
ei from row b in Tables 6 to 8. |
| eb¢i |
multiple of S(x – bar(x))2 [Table 5; Equation 6]. |
| ei |
sum of squares of the factorial coefficients in each
 row of Tables 6 to 8. row of Tables 6 to 8. |
| eq |
ei from row q in Tables 6 to 8. |
| f |
number of responses at each dosage level of a
 preparation; number of replicates or sets. preparation; number of replicates or sets. |
| fS |
number of observations on the Standard. |
| fU |
number of observations on the Unknown. |
| F1 to F3 |
observed variance ratio with 1 to 3 degrees of
 freedom in numerator [Table 9]. freedom in numerator [Table 9]. |
| G1, G2, and G3 |
relative gap in test for outlier [Table 1]. |
| h |
number of Unknowns in a multiple assay. |
| h¢ |
number of preparations in a multiple assay,
 including the Standard and h Unknowns; i.e., including the Standard and h Unknowns; i.e.,
 h¢ = h + 1. h¢ = h + 1. |
| i |
interval in logarithms between successive
 log-doses, the same for both Standard log-doses, the same for both Standard
 and Unknown. and Unknown. |
| k |
number of estimated log-potencies in an average
 [Equation 24]; number of treatments or doses [Equation 24]; number of treatments or doses
 [Table 4; Equations 1, 13, 15, 16]; number of [Table 4; Equations 1, 13, 15, 16]; number of
 ranges or groups in a series [Table 2]; number ranges or groups in a series [Table 2]; number
 of rows, columns, and doses in a single Latin of rows, columns, and doses in a single Latin
 square [Equations 1a, 16a]. square [Equations 1a, 16a]. |
| L |
length of the confidence interval in logarithms
 [Equations 24, 26, 29, 38], or in terms of a [Equations 24, 26, 29, 38], or in terms of a
 proportion of the relative potency of the proportion of the relative potency of the
 dilutions compared [Equations 31, 33]. dilutions compared [Equations 31, 33]. |
| Lc |
length of a combined confidence interval
 [Equations 42, 43]. [Equations 42, 43]. |
| Lc¢ |
length of confidence interval for a semi-weighted
 mean bar(M) [Equation 48]. mean bar(M) [Equation 48]. |
| LD50 |
lethal dose killing an expected 50% of the
 animals under test [Equation 2c]. animals under test [Equation 2c]. |
| M |
log-potency [Equation 2]. |
| M¢ |
log-potency of an Unknown, relative to its
 assumed potency. assumed potency. |
| bar(M) |
mean log-potency. |
| n |
degrees of freedom in an estimated variance s2 or
 in the statistic t or in the statistic t or 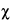 2. 2. |
| n¢ |
number of Latin squares with rows in common
 [Equations 1a, 16a]. [Equations 1a, 16a]. |
| N |
number; e.g., of observations in a gap test
 [Table 1], or of responses y in an assay [Table 1], or of responses y in an assay
 [Equation 16]. [Equation 16]. |
| P |
probability of observing a given result, or of the
 tabular value of a statistic, usually P = 0.05 or tabular value of a statistic, usually P = 0.05 or
 0.95 for confidence intervals [ Tables 1, 2, 9]. 0.95 for confidence intervals [ Tables 1, 2, 9]. |
| P* |
potency, P* = antilog M or computed directly. |
| R |
ratio of a given dose of the Standard to the
 corresponding dose of the Unknown, or assumed potency corresponding dose of the Unknown, or assumed potency
 of the Unknown [Equations 2, 30, 33]. of the Unknown [Equations 2, 30, 33]. |
| R* |
ratio of largest of k ranges in a series to their sum
 [Table 2]. [Table 2]. |
s = 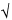 bar(s)2 bar(s)2 |
standard deviation of a response unit, also of a
 single estimated log-potency in a direct assay single estimated log-potency in a direct assay
 [Equation 24]. [Equation 24]. |
| s2 |
error variance of a response unit. |
| Si |
a log-dose of Standard [ Tables 6, 7]. |
| S |
“the sum of.” |
| t |
Student's t for n degrees of freedom and
 probability P = 0.05 [Table 9]. probability P = 0.05 [Table 9]. |
| T |
total of the responses y in an assay [Equation 16]. |
| T ¢ |
incomplete total for an assay in randomized sets
 with one missing observation [Equation 1]. with one missing observation [Equation 1]. |
| T1 |
S(y) for the animals injected with the Standard on
 the first day [Equations 18, 36]. the first day [Equations 18, 36]. |
| T2 |
S(y) for the animals injected with the Standard on
 the second day [Equations 18, 36]. the second day [Equations 18, 36]. |
| Ta |
Ti for the difference in the responses to the
 Standard and to the Unknown [Tables 6 to 8]. Standard and to the Unknown [Tables 6 to 8]. |
| Tab |
Ti for testing the difference in slope between
 Standard and Unknown [Tables 6 to 8]. Standard and Unknown [Tables 6 to 8]. |
| Taq |
Ti for testing opposed curvature in the curves for
 Standard and Unknown [Tables 6 to 8]. Standard and Unknown [Tables 6 to 8]. |
| Tb |
Ti for the combined slope of the dosage-response
 curves for Standard and Unknown [Tables 6 to curves for Standard and Unknown [Tables 6 to
 8]. 8]. |
| Tb¢ |
S(x1Tt) or S(x1y) for computing the slope of the
 log-dose response curve [Equations 10, 23, log-dose response curve [Equations 10, 23,
 28]. 28]. |
| Ti |
sum of products of Tt multiplied by the
 corresponding factorial coefficients in each corresponding factorial coefficients in each
 row of Tables 6 to 8. row of Tables 6 to 8. |
| Tq |
Ti for testing similar curvature in the curves for
 Standard and Unknown [Tables 6 to 8]. Standard and Unknown [Tables 6 to 8]. |
| Tr |
row or set total in an assay in randomized sets
 [Equation 16]. [Equation 16]. |
| Tr¢ |
incomplete total for the randomized set with a
 missing observation in Equation 1. missing observation in Equation 1. |
| Tt |
total of f responses y for a given dose of a
 preparation [Tables 6 to 8; Equations 6, 13, preparation [Tables 6 to 8; Equations 6, 13,
 14, 16]. 14, 16]. |
| Tt¢ |
incomplete total for the treatment with a missing
 observation in Equation 1. observation in Equation 1. |
| Ui |
a log-dose of Unknown [Tables 6 to 8]. |
| v |
variance for heterogeneity between
 assays [Equation 45]. assays [Equation 45]. |
| V = 1/w |
variance of an individual M [Equations 44 to 47]. |
| w |
weight assigned to the M for an individual assay
 [Equation 38], or to a probit for computing an [Equation 38], or to a probit for computing an
 LD50 [Equations 2a, 2b]. LD50 [Equations 2a, 2b]. |
| w¢ |
semi-weight of each M in a series of assays
 [Equations 47, 48]. [Equations 47, 48]. |
| x |
a log-dose of drug in a bioassay [Equation 5];
 also the difference between two log-threshold also the difference between two log-threshold
 doses in the same animal [Equation 12]. doses in the same animal [Equation 12]. |
| x* |
coefficients for computing the lowest and highest
 expected responses YL and YH in a log-dose expected responses YL and YH in a log-dose
 response curve [Table 4; Equation 3]. response curve [Table 4; Equation 3]. |
| x1 |
a factorial coefficient that is a multiple of (x – bar(x))
 for computing the slope of a straight line for computing the slope of a straight line
 [Table 5; Equation 6]. [Table 5; Equation 6]. |
| bar(x) |
mean log-dose [Equation 5]. |
| bar(x)S |
mean log-dose for Standard [Equation 9]. |
| bar(x)U |
mean log-dose for Unknown [Equation 9]. |
| X |
log-potency from a unit response, as interpolated
 from a standard curve [Equations 7a, 7b, 19]. from a standard curve [Equations 7a, 7b, 19]. |
| XM |
confidence limits for an estimated log-potency M
 [Equations 25, 30]. [Equations 25, 30]. |
| XP* |
confidence limits for a directly estimated
 potency P* (see Digitalis assay) [Equation 33]. potency P* (see Digitalis assay) [Equation 33]. |
| y |
an observed individual response to a dose of drug
 in the units used in computing potency and the in the units used in computing potency and the
 error variance [Equations 13 to 16]; a unit error variance [Equations 13 to 16]; a unit
 difference between paired responses in 2-dose difference between paired responses in 2-dose
 assays [Equations 17, 18]. assays [Equations 17, 18]. |
| y1 . . . yN |
observed responses listed in order of magnitude,
 for computing G1, G2, or G3 in Table 1. for computing G1, G2, or G3 in Table 1. |
| y¢ |
replacement for a missing value [Equation 1]. |
| bar(y) |
mean response in a set or assay [Equation 5]. |
| bar(y)t |
mean response to a given treatment
 [Equations 3, 6]. [Equations 3, 6]. |
| Y |
a response predicted from a dosage-response
 relationship,often with qualifying subscripts relationship,often with qualifying subscripts
 [Equations 3 to 5]. [Equations 3 to 5]. |
| z |
threshold dose determined directly by titration
 (see Digitalis assay) [Equation 11]. (see Digitalis assay) [Equation 11]. |
| bar(z) |
mean threshold dose in a set (see Digitalis assay)
 [Equations 31, 32, 33]. [Equations 31, 32, 33]. |